[C/C++] 백준 1197번(최소 스패닝 트리) & 크루스칼 알고리즘

문제

https://www.acmicpc.net/problem/1197

입력

첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

출력

첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.

예제

풀이(코드)

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// Global variable
int V, E;
vector<pair<int, pair<int, int>>> edge;
vector<int> par;
long long res;

// Function
void init() {
    ios::ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}
int findParent(int a){
    if(par[a] == a) return a;
    else return par[a] = findParent(par[a]);
}
bool isSameParent(int a, int b) {
    int par_a = findParent(a);
    int par_b = findParent(b);
	
    // 둘의 부모가 같으면 true, 아니면 false
    return par_a == par_b;
}
void uni(int a, int b) {
    int par_a = findParent(a);
    int par_b = findParent(b);
    par[par_b] = par_a;
}
void MST() {
    for(int i=0; i<edge.size(); i++) {
        int cur_a = edge[i].second.first;
        int cur_b = edge[i].second.second;

        if(!isSameParent(cur_a, cur_b)) {
            // union tree
            uni(cur_a, cur_b);
            res += edge[i].first;
        }
    }
    
}

int main() {
    init();
    cin >> V >> E;
    for(int i=0; i<=E; i++) { par.push_back(i); }
    
    // 입력
    for(int i=0; i<E; i++) {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        edge.push_back({w, {v1, v2}});
    }
    // 가중치가 낮은 순으로 간선을 정렬
    sort(edge.begin(), edge.end());
    MST();
	
    // 출력
    cout << res;
    
    return 0;
}

크루스칼 알고리즘

 크루스칼 알고리즘은 모든 노드들을 최소의 비용으로 연결하는 최소 신장 트리(Minimim Spanning Tree, MST)를 구하는 대표적인 알고리즘이다. 

동작방식

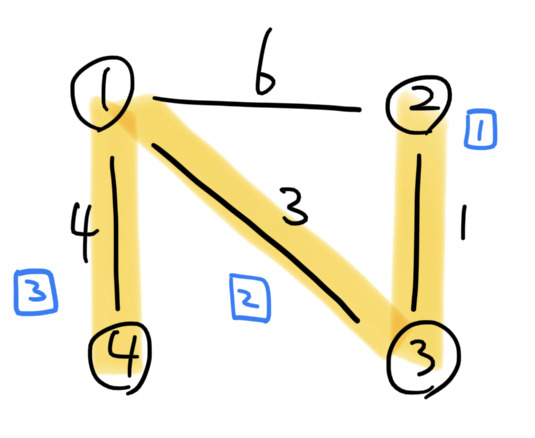
주어진 간선정보(정점1, 정점2, 가중치)를 가중치 순으로 정렬하여 값이 낮은 간선들을 차례대로 연결해주면 된다.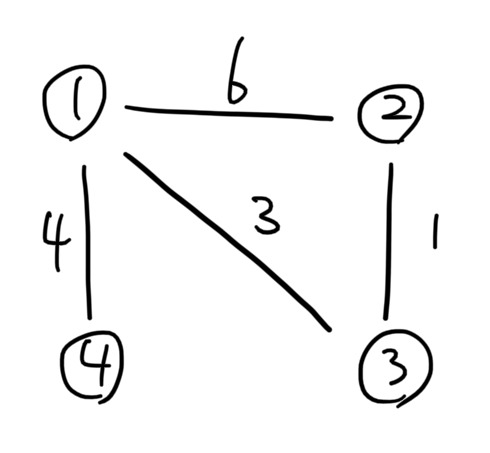

위의 그림에서 주어진 간선 정보가

• (1 - 2), 6
• (1 - 3), 3
• (1 - 4), 4
• (2 - 3), 1

이렇게 있다면 이를 가장 우측 데이터인 가중치로 정렬을 해준 다음 가중치가 낮은 순으로 방문해준다.

시작은 간선은 없고 노드만 있다 생각하면 되고, 가중치가 낮은 순서대로 방문을 하면 파란색 숫자로 적힌 1, 2, 3번 순으로 방문한다. 4번을 방문하지 않는 이유는 이미 1 - 2 사이 갈 수 있는 방법이 있기에 새로운 간선은 연결해주지 않는것이다. 

정리해보자면

1. 입력받은 간선 정보를 가중치 순으로 정렬 및 값이 낮은 간선부터 탐색
2. 두 노드가 포함된 트리의 부모노드를 비교(Find)
   1. 만약 같다면 이미 연결되어있는 노드이기에 Pass
   2. 다르다면 두 노드를 연결해주고 부모노드를 한쪽으로 통일해준다.(Union)
3. 입력받은 간선의 크기만큼 반복해준다.

위의 과정을 거처 모든 노드를 연결하는 하나의 트리를 만드는 것이 크루스칼 알고리즘의 목적이다.

시간복잡도

간선을 탐색하는데 걸리는 시간 O(E), find-union을 하고 merge하는데 소요되는 시간은 O(1), 간선을 오름차순으로 정렬하는데 소모되는 시간 O(E logE)이고, 이 중 정렬하는 시간이 지배적이기에 크루스칼 알고리즘의 시간복잡도는 O(E logE)이다.